システムプログラムでは正確な数値を表せる桁数に限界があります。
精度の高い小数を扱う場合は、技術的にどれくらいの精度(桁数)を保証できるか、あるいはどこまでの精度を保証すべきかが仕様決定の上で重要となります。
ここではシステムの構成要素であるプログラミング言語やデータベース等の観点から保証可能な有効桁数について解説いたします。
プログラミング言語の観点
ほぼすべてのプログラミング言語は IEEE 754 標準で定義されている浮動小数点数に基づいて小数を扱います。
通常は単精度(float)が 32bit、倍精度(double)が 64bit の全長を持っています。
IEEE 754-2008 リビジョン
https://en.wikipedia.org/wiki/IEEE_754-2008_revision
浮動小数点数は符号部、指数部、仮数部の3つの部分で構成されます。
| 全長 [bit] | 符号部 [bit] | 指数部 [bit] | 仮数部 [bit] | |
|---|---|---|---|---|
| 単精度 | 32 | 1 | 8 | 23 |
| 倍精度 | 64 | 1 | 11 | 52 |
実際の数値データは仮数部が保持するため、プログラム上の浮動小数点数は倍精度の場合、52bit で表されることになります。
52bit で表すことのできる小数の限界(有効桁数)は以下の計算で求められます。
有効桁数 \(= 52 [bit] × \log _{10}2 \fallingdotseq 15.65 \)
したがってプログラムで小数を扱う場合の有効桁数の最低ラインは 15 桁となりますが、末尾の数値は丸め誤差が生じる可能性があるため、確実に正確な値を表現できる桁数は 14 桁になります。
例えば PHP ではprecisionという設定オプションにより浮動小数点の最大桁数を指定できますが、デフォルト値は 14 となっています。
このとき、15 桁以上の小数を扱おうとすると、15 桁目の数値を四捨五入し 14 桁に丸められます。
ただし浮動小数点数の丸め方については、IEEE 754 で「偶数への丸め」が推奨されており、単純な四捨五入ではありません。
echo 12.3456789012345678; // 12.345678901235と表示される
echo 123.456789012345678; // 123.45678901235
// 偶数への丸め
echo 12.3456789012345; // 12.345678901234 末尾が切り捨てprecisionの値を増やすと15 桁以上の小数を扱うことができますが、内部的な計算精度は変わらないことに注意してください。
ini_set('precision', 20);
echo 12.3456789012345678; // 12.345678901234567348
echo 123.456789012345678; // 123.45678901234568059
echo 12.3456789012345; // 12.34567890123449984715 桁目以降は信頼できる数値にならないため、15 桁以上の小数は異常値として入力を拒否すべきでしょう。
以下は有効桁数に収まっているかどうかの判定メソッドの例です。
function isValidPrecision($number, $digit=14){
$str = (string)$number;
$str = str_replace('-', '', $str);
$str = str_replace('.', '', $str);
return strlen($str) <= $digit;
}
なお丸め誤差は、有効桁数と関係なく四捨五入や切り上げ・切り捨てなどの丸め処理を行うことにより発生する場合があります。
これは無限循環小数となる数値が2進数と10進数で異なることに起因します。
例えば 1/10 は10進数では割り切れますが、2進数では割り切れず無限循環小数となります。
// 小数点以下20桁まで表示
echo sprintf("%.20f", 0.1); // 0.10000000000000000555普段は見えない 15 桁以降の誤差が数値計算や丸め処理によってあらわれてきます。
以下は消費税の計算で発生する丸め誤差の例です。
割り切れているはずの数値が2進数の計算で端数が出て、これを切り上げることにより得られる結果が変わっています。
$price = 225; // 値段225円
$tax = 0.08; // 消費税8%
// 小数点以下切り上げ
$total = $price * (1 + $tax); // 243
$amount = ceil($total); // 244 ★
echo sprintf("%.20f", $total); // 243.00000000000002842171この問題はBCMathなどの数値計算ライブラリを使用することで回避できます。
$price = 225; // 値段225円
$tax = 0.08; // 消費税8%
// 任意精度数値の乗算
$total = bcmul((string)$price, (string)(1 + $tax), 20); // 243.00000000000000000000
$amount = ceil((float)$total); // 243BCMathを使用することにより、15 桁以上の小数を扱えるようになります。
ただし全体の桁数でなく、小数部の最大桁数が必要になることに注意してください。
$a = '12.3456789012345678';
$b = '123.456789012345678';
$c = '123.456789012345';
echo bcadd($a, '0', 15)."<br>\n"; // 12.345678901234567
echo bcadd($b, '0', 15)."<br>\n"; // 123.456789012345678
echo bcadd($c, '0', 15)."<br>\n"; // 123.456789012345000プログラミング言語の観点からの結論としては以下となります。
・高精度な要求仕様がなければ 14 桁の範囲に収める
・高精度が必要であれば小数部の有効桁数を決定した上で数値計算ライブラリを使用する
データベースの観点
データベースも IEEE 754 準拠であり、おおよそ前項で述べたことと同じことがデータベースにもあてはまります。
浮動小数点型には単精度(32bit)と倍精度(64bit)があり、倍精度だと仮数部に 52bit が割り当てられ、有効桁数が約 15 桁になります。
ただし末尾の数値は丸め誤差が生じる可能性があるため、実際に正確な値を表現できる桁数は 14 桁になります。
| 単精度型名 | 倍精度型名 | 倍精度の有効桁数 | |
|---|---|---|---|
| MySQL | FLOAT | DOUBLE | 14 |
| PostgreSQL | REAL | DOUBLE PRECISION | 14 |
以下は MySQL で 15 桁以上の小数を浮動小数点型のカラムに保存した場合です。
>insert into Test values(12.3456789012345678901234); // 24桁
+--------------------+
| double_column |
+--------------------+
| 12.345678901234567 | # 17桁
+--------------------+17 桁の数値が格納されますが、数値によっては丸め誤差が生じるため、信頼できるのは 14 桁までです。
>insert into Test values(0.12345678901234567); # 17桁
>select * from Test;
+---------------------+
| double_column |
+---------------------+
| 0.12345678901234566 | # この例では17桁目がおかしい
+---------------------+有効桁数と関係なく、四捨五入や切り上げ・切り捨てなどの丸め処理を行うことにより丸め誤差が発生します。
>select ceiling(225 * 1.08e0) as result;
+--------+
| result |
+--------+
| 244 | # 243が正しい
+--------+15 桁以上の小数を扱いたい場合は、固定小数点型(DECIMAL)を利用します。
固定小数点型では全体の最大桁数と小数部の最大桁数を指定します。
ちなみに指定可能な最大桁数は以下の通りです。
| 固定小数点型名 | 全体の最大桁数 | 小数部の最大桁数 | |
|---|---|---|---|
| MySQL | DECIMAL | 65 | 30 |
| PostgreSQL | DECIMAL/NUMERIC | 131,072 | 16,383 |
固定小数点型では 15 桁以上の小数を扱えるというだけでなく、丸め誤差も発生しません。
ただ、数値の範囲が見積れないからといってむやみに桁数を大きくしてしまうと、メモリを大量に消費してしまうため注意が必要です。
概算になりますが、1桁につき 1byte 消費すると計算すると、例えば 65 桁を設定した場合 65byte が必要となると考えられます。
この消費量はVARCHAR型やTEXT型のように実際のデータ長によって最適化されません。
固定小数点型では正確な計算が可能となりますが、プログラム側で高精度に対応するため数値計算ライブラリの使用が必須となります。
数値計算ライブラリは小数を文字列に置き換えるため、データベース側で当該カラムに関する数値計算をさせる場合を除き、小数は文字列として保存しても問題ないかもしれません。VARCHAR型やTEXT型の使用メモリ量は文字長に比例するため、こちらの方がメモリ使用量が少なくて済むでしょう。
データベースの観点からの結論としては以下となります。
・高精度な要求仕様がなければ 14 桁の範囲に収める
・高精度が必要であれば整数部と小数部の有効桁数を決定した上で固定小数点型を使用する
・高精度な固定小数点型を使用する場合はプログラム側で数値計算ライブラリを使用する
・データベース側で数値計算をさせない場合は小数を文字列として保存すべきか検討する
CSV ファイルのインポート
システムによっては入力値を CSV ファイルから取り込む場合も想定されます。
しかし CSV ファイルの編集作業というのは、IT リテラシーのそれほど高くない一般利用者にとっては思いのほか敷居が高く、オペミスを誘発しやすい作業であることを念頭に置いておく必要があるかもしれません。
CSV ファイルはテキスト形式であり、一般のテキストエディタであれば編集が可能ですが、Windows ではデフォルトで Microsoft Excel に関連付けられており、そのまま Excel で編集作業を行う利用者も多いのではないでしょうか。
ここで問題となってくるのは Excel の仕様です。
なんの設定変更も行わず使用する場合、セルの書式設定は「標準」の表示形式になっており、整数値は 11 桁、小数だと 9 桁までしか表示できません。
CSV ファイルを開いて保存するだけでもすべての小数が 9 桁に丸められてしまいます。
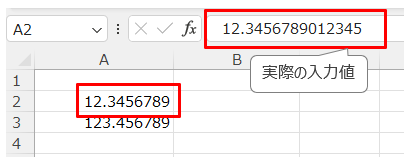
この問題は、表示形式を「数値」あるいは「文字列」とすることで一時的に解決できます。
該当のセルを選択し、「セルの書式設定」を選択して表示形式を「数値」にすることで小数点以下の桁数を指定できるようになります。
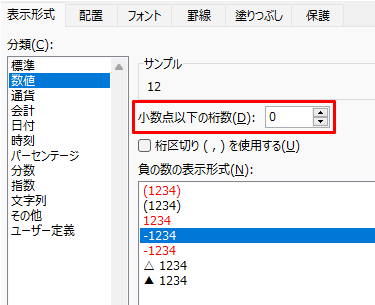
文字列として保存する場合は、セルの書式設定で表示形式を「文字列」とするか、数値の先頭にシングルクォート(アポストロフィー)をつけます。
※ダブルクォートで囲っても文字列にはなりません。
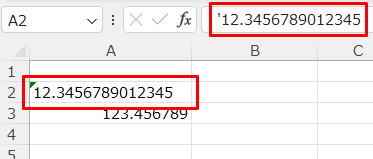
しかし、この方法が有効なのは1回限りです。
設定そのものは CSV ファイルには保存されないため、次に開いたときには表示形式は「標準」に戻り、また 9 桁に丸められてしまいます。
したがって編集のたびに再度設定し直す必要があります。
もし利用者に負担をかけないようにするのであれば、有効桁数は 9 桁にすべきです。
10桁以上の小数を扱いたいのであれば、これらのルールを利用者に求めるか、CSV ファイル専用のエディタを利用してもらうしかないでしょう。
QuickSight の観点
QuickSight を利用した場合の有効桁数はどうなるでしょうか。
公式ドキュメントがいまいち要領を得なかったので、MySQL と繋げたデータセットで実測した情報を元に解説します。
サポートされているデータ型と値
https://docs.aws.amazon.com/quicksight/latest/user/supported-data-types-and-values.html
https://docs.aws.amazon.com/ja_jp/quicksight/latest/user/supported-data-types-and-values.html
QuickSight では、データセットのフィールドで「10進数」のデータタイプを設定することにより小数を扱えます。
さらに SPICE を利用している場合は、固定小数点と浮動小数点が選択できます。
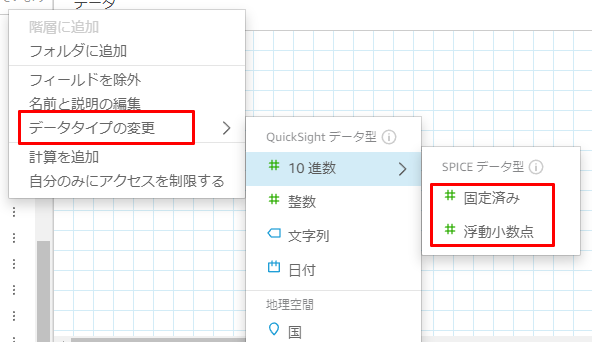
直接クエリでは浮動小数点型のカラムは MySQL の最大値でもある 17 桁、固定小数点型では小数点以下4桁に丸められるようでした。
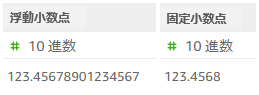
ただ、分析のデータメニューで表示内容の小数点以下の桁数を変更したところ、固定小数点型も 17 桁までは実値として内部保持しているようでした。
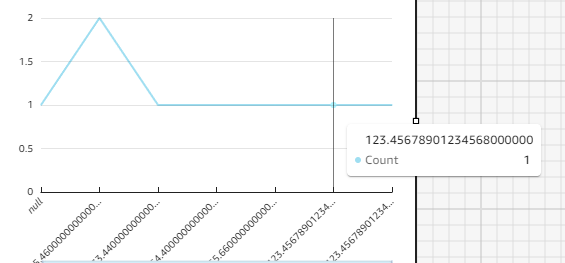
これは MySQL 側で小数を文字列として保存し、QuickSight 側のフィールド設定で「10進数」に変換した場合も同様の結果でした。
さらに計算フィールドを使用してもやはり 17 桁でした。
ちなみに小数点以下の桁数変更の手順としては、該当のカラムの右側(…)をクリックし「形式」→「その他のフォーマットオプション」を選択、小数位のカスタムを選択し、桁数を設定します。
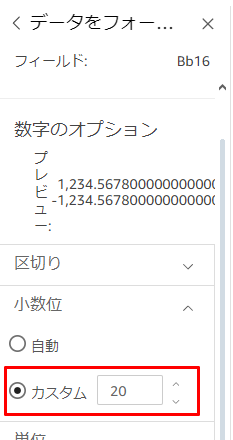
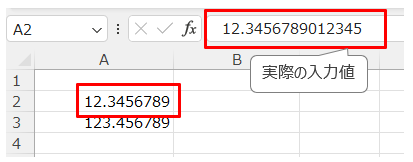
SPICE を利用したデータセットについてもほぼ同じ結果であり、違いは固定小数点型は小数点以下4桁に完全に丸められてしまうところでした。
以上のことから QuickSight における小数の有効桁数は 17 桁であり、固定小数点型は高精度(桁数増加)の要件に寄与しないという結果となりました。

コメント