デシジョンテーブルとは

デシジョンテーブルの作り方やテスト条件の組み合わせパターンが増えすぎた場合の対処方法などを説明します。

複数の入力条件が重なり合うプログラムの機能テスト（ブラックボックステスト）を実施する際、入力条件の組み合わせパターンを網羅した表を作成し、パターンの視認性を上げることで確認漏れを防止します。
デシジョンテーブル【Decision Tables】とは、この「組み合わせの総当たり表」のことであり、「決定表」（JIS X 0125）として規格が定められています。
デシジョンテーブルを作成することにより複雑な条件を整理することができるので、複数条件の組合せを漏れなく洗い出すことができます。

例としてネットショッピングで商品を購入する際の配送料を算出するプログラムのデシジョンテーブルを見てみましょう。
※配送料の計算方法についてはニトリの公式通販を参考にしていますが、説明のために一部簡略化しています。
※説明の便宜のため、１つの商品に対する配送料の計算だけに絞っています。

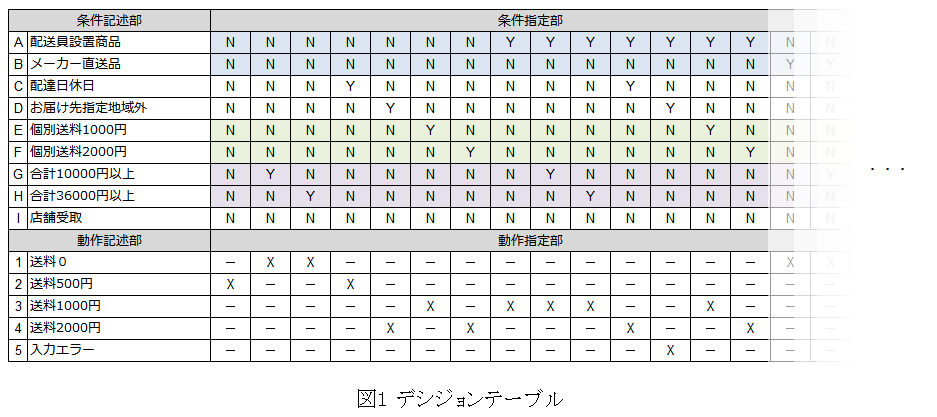
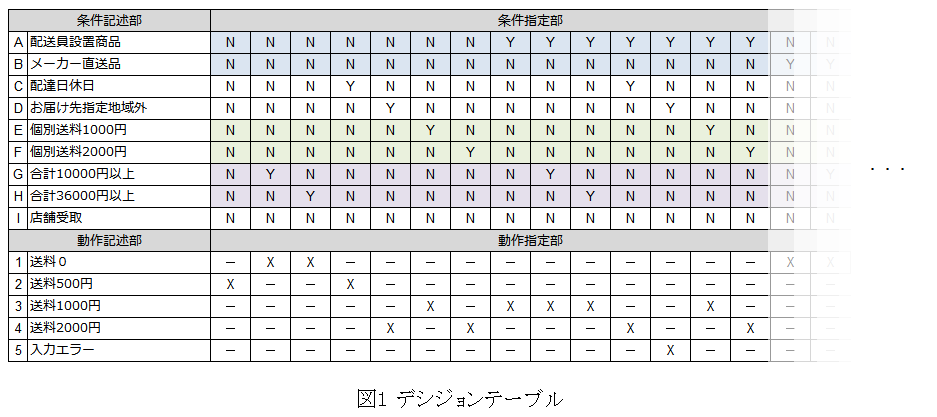
デシジョンテーブルには条件を記述する箇所（条件記述部）と、その条件に対する動作を記述する箇所（動作記述部）があり、条件指定部でそれぞれの条件に適合するか否か（Y/N）の組み合わせを指定し、動作指定部でどの動作に適合するかを X（eXecute）で指定します。
なお、このデシジョンテーブルでは組み合わせとしてあり得ないパターン（禁則）が存在します。
例えば個別送料が 1,000 円で設定され、かつ 2,000 円でも設定されている、という状況はあり得ません。
図１では同時に Y にならない部分を色分けしています。

一般的にデシジョンテーブルはこのようなフォーマットで表されますが、条件記述部の書き方に少々違和感を感じないでしょうか。
これは条件指定部が Y/N の２値しかとれないため、条件記述部に複数の条件因子とその内容の組み合わせを列挙しなければならなくなってしまっているからです。
条件の組み合わせは条件指定部でのみ表されるべきであり、以下のように条件の因子ごとに分類されている方が直観的で理解しやすかと思います。

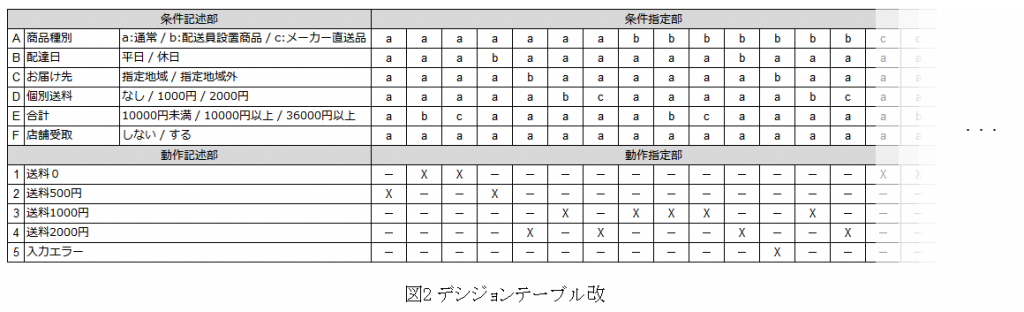
条件記述部が条件の因子とその内容に分かれてすっきりしました。
旧フォーマットでは色分けしていた組み合わせとしてあり得ないパターンもこのフォーマットでは気にする必要がなくなっています。
本サイトでは、デシジョンテーブルのフォーマットについてはこちらを採用したいと思います。


以下、説明の便宜のため、テスト条件を因子、その条件の内容を水準と呼びます。

実験計画法とは、効率のよい実験方法を設計（デザイン）し、結果を適切に解析することを目的とする統計学の応用分野です（wikipedia）。
実験計画法では、テスト条件を因子といい、その条件の内容を水準といいます。
水準は例えば入力の選択肢であったり、同値分割に基づく境界値などになります。

参考： 同値分割とは（単体テストのテスト項目の観点）

パターン数を減らす方法
条件指定部の組み合わせは基本的には総当たりなので、図２の例でいうと、3x2x2x3x3x2 = 216 通り の組み合わせが存在することになります。

組み合わせ数 ＝ 各因子の水準数（内容の数）の掛け算

図１（旧フォーマット）では組み合わせ数が９通りなので、2⁹ = 512 通りですが、同時に Y にならないパターンを除くと 216 通りとなります。

計算式を見ればわかると思いますが、入力条件の数によって組み合わせのパターン数があっという間に膨大な数になるため、実際のテストにおいてはすべての条件の組み合わせを実施することが困難な場合があります。
このような場合には、なんらかの方法で組み合わせのパターン数を減らす必要があります。
とはいえ、ただやみくもにパターンを減らしてもテスト項目の網羅性は担保されません。
そこには「テストとして十分である」という根拠が必要です。
ではどのようにして組み合わせパターンを間引くと良いでしょうか。
以下に２つの方法論を紹介します。

因子をグループ分けする（デシジョンテーブルを分ける）
因子の数が多い場合には以下のような観点に基づき、因子の数を減らします。

・プログラムロジック上あまり重要でないもの
・他の因子との関係性の弱いもの

減らした因子は別々にテストを行うか、もしくは上記の観点から関係性の強いもの同士を分類し、別々のデシジョンテーブルにすると良いでしょう。
この重要性や関係性の判定は、ビジネスロジック（業務論理）やアルゴリズムから判断します。

例えば図２の例でいうと、以下のように分けることができると思います。

テーブル名	組み合わせる因子	組み合わせ数
DTABLE 1	店舗受取（因子F）	2 通り
DTABLE 2	商品種別（因子A）、配達日（因子B）、お届け先（因子C）	12 通り
DTABLE 3	商品種別（因子A）、個別送料（因子D）、合計（因子E）	27 通り

表1 組み合わせる因子の分け方

DTABLE 1
因子 F「店舗受取」は水準 b「する」の時点で他のすべての条件が無効になるため、他の因子と組み合わせる重要性があまりありません。

DTABLE 2
因子B「配達日」と因子 C「お届け先」は、水準 A-b「商品種別：配送員設置商品」としか関係性がないため、因子 A「商品種別」との組み合わせを検証すればテストとしてはまずまずであると判断できます。
水準を A-b に固定しても良いかもしれません。

DTABLE 3
DTABLE 1, 2 で組み合わせた因子以外（D, E）と、因子 D「個別送料：なし」と関係性の強い因子 A「商品種別」の組み合わせを検証します。

上記のように因子を分けることで、組み合わせ数は 216 → 41 通りになりました。
もちろん組み合わせを減らすことによってこのパターン以外で障害が発生する可能性はでてきますが、概ね網羅性の高いテスト項目を作成することができたかと思います。

ペアワイズ法によって組み合わせパターンを制限する
因子の関係性がフラットで分類が難しい場合、ペアワイズ法【Pairwise Testing】（オールペア法）を利用して因子の組み合わせ数を制限します。
ペアワイズ法とは２因子間の組み合わせだけは全て網羅するよう組み合わせパターンを考慮するもので、ほとんどの障害は最大2つの要因の相互作用によって引き起こされるという観察に基づく効果的なテストケース生成手法です。

Pairwise (a.k.a. all-pairs) testing is an effective test case generation technique that is based on the observation that most faults are caused by interactions of at most two factors. Pairwise-generated test suites cover all combinations of two therefore are much smaller than exhaustive ones yet still very effective in finding defects.
ペアワイズ（別名オールペア）テストは、ほとんどの障害は最大2つの要因の相互作用によって引き起こされるという観察に基づく効果的なテストケース生成手法です。ペアワイズで生成されたテストスイートは2つの組み合わせをすべてカバーするため、網羅的なものよりもはるかに小さく、それでも欠陥を見つけるのに非常に効果的です。

Pairwise Testing

なおペアワイズ法は、組み合わせを均一にすることによりランダムにパターンを減らすよりもテスト項目として効果的と言えますが、これで完全なテストケースが生成できると考えてはいけません。
もしテスト項目として十分でないと考えられるのであれば、組み合わせる因子の数を３つに増やすなどの工夫が必要になります。
ちなみにペアワイズ法によって組み合わせパターンを間引いた結果、組み合わせ数は 216 → 9 通り にまで減ってしまいました。

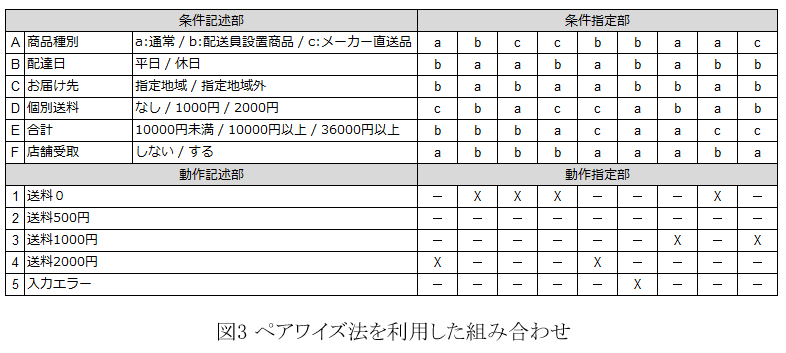
うーむ、因子 F のせいであまり効果的な組み合わせが少ないような気がしますね……。
ペアワイズ法を利用するのであれば、因子 F を取り除いたデシジョンテーブルの方が良さそうです。
ちなみに組み合わせる因子数を３とした場合は、29 通りとなります。

参考までに図３の内容を元に Excel でデシジョンテーブルのサンプルを作成してみました。

ペアワイズ法で使用するツール
ペアワイズ法による組み合わせパターンを手作業で生成するのは大変ですが、PICT という便利なツールがあります。
次ページでは、PICT について詳しく解説したいと思います。

参考： 組み合わせテストパターン抽出ツール PICT とは
参考： デシジョンテーブル自動生成（PICT を利用したサンプル）

・GitHub
Microsoft / pict

・Windows 版（MSI イメージ）
http://download.microsoft.com/download/f/5/5/f55484df-8494-48fa-8dbd-8c6f76cc014b/pict33.msi